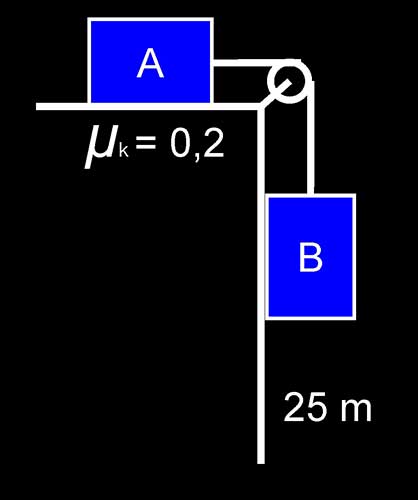


Hukum Newton Ketiga (Hukum Aksi-Reaksi)

Hukum Newton Kedua (Gaya, Massa, dan Percepatan)

Dinamika: Hukum Newton Pertama (Inersia)
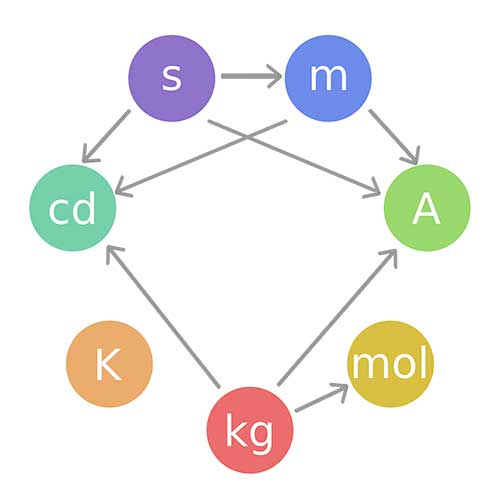
Notasi Ilmiah dan Konversi Satuan

Angka Penting, Operasi Hitung, dan Pembulatan
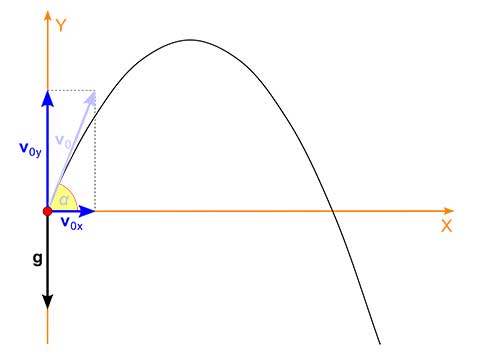
Kinematika (2D): Gerak Parabola | Gerak Peluru
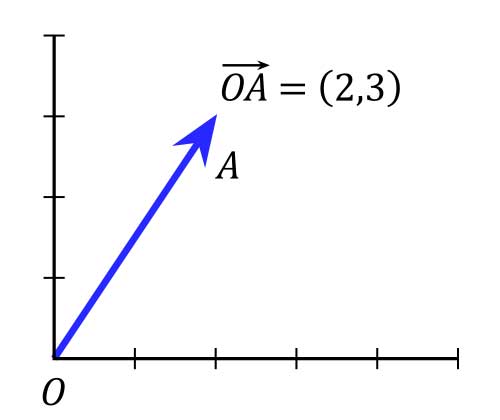
Kinematika (2D): Vektor Posisi, Perpindahan, Kecepatan, dan Percepatan

Gerak Melingkar Berubah Beraturan (GMBB)
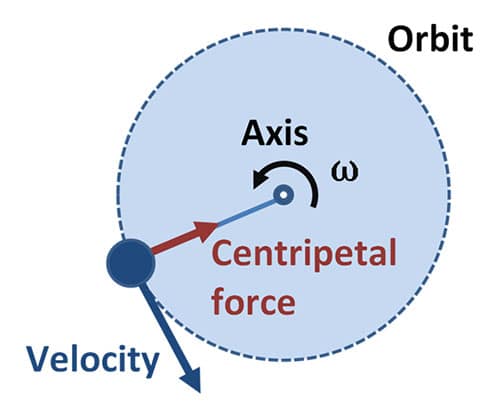
Gerak Melingkar Beraturan (GMB)

Gerak Lurus Berubah Beraturan (Percepatan Tetap)

Gerak Lurus Beraturan (Kecepatan Tetap)
Menghitung Besar dan Arah Resultan Vektor
Menyelesaikan Persamaan Eksponen

Teori Atom Bohr (Tata Surya)
Rumus Umum Bentuk Akar (Radikal)
Rumus Umum Eksponen
Pengenalan Eksponen
Apakah benda yang berat jatuh lebih cepat?

