Kinematika (2D): Vektor Posisi, Perpindahan, Kecepatan, dan Percepatan

Pada bagian ini kita akan membahas mengenai kinematika gerak translasional (dua dimensi) dengan analisis vektor, sebelum masuk ke perhitungan ada baiknya kita mengetahui definisi dan formulasi rumus-rumus. Kinematika adalah cabang dari mekanika klasik yang mendeskripsikan gerak dari titik, objek, atau sistem (kelompok objek) tanpa mempertimbangkan penyebab dari gerak tersebut. ^[1] Gerak translasional adalah gerak yang melibatkan pergeseran objek pada satu dimensi atau lebih (sumbu x, y, atau z). ^[2]

1. Vektor Posisi

Penulisan vektor dapat dilakukan dengan berbagai cara, tetapi yang umumnya digunakan dalam kinematika adalah penulisan dengan vektor satuan.

\(\mathbf{r} = x\mathbf{i} + y\mathbf{j}\)

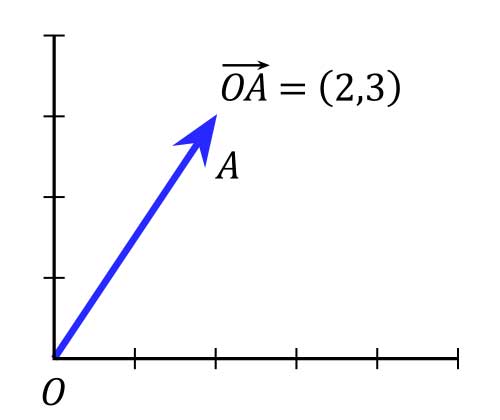
Sehingga gambar di atas dapat dituliskan dengan \(\mathbf{r} = 2\mathbf{i} + 3\mathbf{j}\)

2. Perpindahan

Perubahan posisi pada gerak dua dimensi dapat dicari menggunakan rumus berikut ini:

\(\Delta\mathbf{r} = \mathbf{r}_2 - \mathbf{r}_1\)

• \(\mathbf{r}_1\) adalah posisi awal
• \(\mathbf{r}_2\) adalah posisi akhir

Mari kita coba kerjakan contoh soal berikut:

Sebuah partikel bergerak dalam bidang-XY dari suatu titik dengan koordinat (-3,5) m menuju titik dengan koordinat (-1,-8). Tuliskan (a) vektor posisi dan (b) vektor perpindahannya.

a) Vektor Posisi
\(\mathbf{r}_1 = (-3\mathbf{i} + 5\mathbf{j})\) m
\(\mathbf{r}_2 = (-1\mathbf{i} - 8\mathbf{j})\) m

b) Perpindahan
\(\Delta\mathbf{r} = \mathbf{r}_2 - \mathbf{r}_1\)
\(\Delta\mathbf{r} = (-1-(-3))\mathbf{i} + (-8-5)\mathbf{j}\)
\(\Delta\mathbf{r} = (2\mathbf{i} - 13\mathbf{j})\) m

3. Kecepatan rata-rata

Kecepatan rata-rata pada gerak dua dimensi dapat dicari menggunakan rumus:

\[\mathbf{\bar{v}} = \frac{\Delta\mathbf{r}}{\Delta t} = \ \frac{\mathbf{r}_2 - \mathbf{r}_1}{t_2 - t_1}\]

maka persamaan dapat dituliskan menjadi

\(\mathbf{\bar{v}} = \bar{v}_x \mathbf{i} + \bar{v}_y \mathbf{j}\)

Dari persamaan ini, coba carilah vektor kecepatan rata-rata apabila dalam contoh soal sebelumnya waktu yang diperlukan untuk berpindah adalah 2 sekon.

\[\mathbf{\bar{v}} = \frac{2\mathbf{i} - 13\mathbf{j}}{2} = \ \mathbf{i} - 6,5\mathbf{j} \ m/s\]

4. Kecepatan sesaat

Misalkan seseorang berlari dengan lintasan lurus 100 meter, dan waktu yang diperlukan untuk orang tersebut sampai ke garis finish adalah 20 sekon. Dari situ dapat diketahui kecepatan rata-ratanya adalah 5 m/s, lalu bagaimana cara menghitung kecepatan pada saat \(t\)? Kita bisa mengatakan kecepatan sesaat pada \(t=4 \ s\) adalah juga 5 m/s bila orang tersebut berlari dengan kecepatan konstan, tetapi apakah itu mungkin? Kita tahu kecepatan orang berlari akan berubah-ubah tergantung pada mental dan fisik 🙂

Diperlukan kalkulus untuk menghitung kecepatan sesaat:

\[\mathbf{v} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{r}}{\Delta t} = \frac{d\mathbf{r}}{dt}\]

Dalam gerak dua dimensi ini, posisi juga dapat dinyatakan dalam fungsi posisi terhadap waktu. Sebelum kita mencoba mengerjakan contoh soal dua dimensi, mari kita coba kerjakan soal satu dimensi.

Misalkan partikel bergerak pada sumbu-x dengan persamaan \(x(t) = (6t^2 + t + 8)\) m, hitunglah (a) posisi pada saat \(t = 3 \ s\), (b) persamaan kecepatan, (c) kecepatan pada saat \(t = 3 \ s\).

a) Posisi pada saat \(t=3\) dapat dicari dengan memasukkan angka 3 ke dalam persamaan

\(x(3) = 6.9 + 3 + 8 = 65 \ m\)

b) Persamaan kecepatan dapat dicari dengan turunan

\[\frac{dx}{dt} = 12t + 1\]

c) Kecepatan pada saat \(t = 3 \ s\) dapat dicari dengan memasukkan angka 3 ke dalam persamaan

\(v(t) = 12(3) + 1 = 37 \ m/s\)

Mari kita coba selesaikan contoh soal kecepatan sesaat pada gerak dua dimensi.

Posisi sebuah partikel yang bergerak pada bidang-XY dinyatakan dalam \(\mathbf{r} = (t^3 - 2t^2)\mathbf{i} + (3t^2) \mathbf{j}\), \(\mathbf{r}\) dalam meter dan \(t\) dalam sekon. Carilah (a) vektor kecepatan partikel dan (b) besar kecepatannya pada saat \(t = 2 \ s\).

a) Vektor kecepatan dapat dicari dengan menggunakan turunan
\[\frac{d\mathbf{r}}{dt} = (3t^2 - 4t)\mathbf{i} + (6t) \mathbf{j}\] \(\mathbf{v}_{(2)} = (12 - 8)\mathbf{i} + (12) \mathbf{j}\)
\(\mathbf{v}_{(2)} = (4)\mathbf{i} + (12) \mathbf{j}\)

b) Besar kecepatan dapat dicari dengan rumus besar resultan vektor
\[v_{(2)} = \sqrt{4^2 + 12^2}\] \[v_{(2)} = \sqrt{16 + 144} = \ \sqrt{160} \approx \ 12,65 \ m/s\]

5. Percepatan rata-rata

Percepatan rata-rata pada gerak dua dimensi dapat dicari menggunakan rumus:
\[\mathbf{\bar{a}} = \frac{\Delta\mathbf{v}}{\Delta t} = \ \frac{\mathbf{v}_2 - \mathbf{v}_1}{t_2 - t_1}\]

maka persamaan dapat dituliskan menjadi

\(\mathbf{\bar{a}} = \bar{a}_x \mathbf{i} + \bar{a}_y \mathbf{j}\)

6. Percepatan sesaat

Dengan konsep yang sama dengan kecepatan sesaat, diperlukan kalkulus untuk menghitung percepatan sesaat:

\[\mathbf{a} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{v}}{\Delta s} = \frac{d\mathbf{v}}{dt}\]

Mari kita coba selesaikan contoh soal berikut.

Posisi sebuah partikel yang bergerak pada bidang-XY dinyatakan dalam \(\mathbf{r} = (t^3 - 2t^2)\mathbf{i} + (3t^2) \mathbf{j}\), \(\mathbf{r}\) dalam meter dan \(t\) dalam sekon. Carilah (a) vektor percepatan partikel dan (b) besar percepatannya pada saat \(t = 2 \ s\).

a) Kita telah mengerjakan sampai dengan kecepatan pada soal sebelumnya, saatnya untuk menurunkan lagi.
\[\frac{d\mathbf{r}}{dt} = (3t^2 - 4t)\mathbf{i} + (6t) \mathbf{j}\] \[\frac{d\mathbf{v}}{dt} = (6t - 4)\mathbf{i} + (6) \mathbf{j}\] \(\mathbf{a}_{(2)} = (12 - 4)\mathbf{i} + (6) \mathbf{j}\)
\(\mathbf{a}_{(2)} = (8)\mathbf{i} + (6) \mathbf{j}\)

b) Besar percepatan dapat dicari dengan rumus besar resultan vektor
\[a_{(2)} = \sqrt{8^2 + 6^2}\] \[a_{(2)} = \sqrt{64 + 36} = \ \sqrt{100} = \ 10 \ m/s^2\]

Video di bawah ini akan mencoba menghitung percepatan lompatan belalang 🙂