Gerak melingkar berubah beraturan adalah gerak objek pada lintasan lingkaran dengan percepatan sudut \(\alpha\) tetap. Percepatan sudut yang konstan ini membuat kecepatan sudut \(\omega\) berubah setiap detik, bisa lebih cepat atau lebih lambat, tergantung tanda positif/negatif pada percepatan sudut \(\alpha\).
Sama dengan artikel gerak melingkar beraturan (GMB) sebelumnya, hubungan-hubungan besaran pada gerak melingkar berubah beraturan (GMBB) juga memiliki persamaan dengan gerak lurus berubah beraturan (GLBB). Berikut ini adalah perbandingan GLBB dan GMBB: [1]
Persamaan Kinematika Rotasi
| Linier/translasional | Angular/rotasional |
|---|---|
| \(x = v . t\) | \(\theta = \omega . t\) |
| \(v_t = v_0 + a . t\) | \({\omega}_t = {\omega}_0 + \alpha . t\) |
| \(x = v_0 . t + \frac{1}{2} a . t^2\) | \(\theta = {\omega}_0 . t + \frac{1}{2} \alpha . t^2\) |
| \({v_t}^2 = {v_0}^2 + 2a . x\) | \({{\omega}_t}^2 = {{\omega}_0}^2 + 2\alpha . \theta\) |
Di mana:
- \(\theta\) adalah besar sudut lintasan melingkar yang ditempuh.
- \({\omega}_0\) adalah kecepatan sudut awal.
- \({\omega}_t\) adalah kecepatan sudut akhir.
- \(\alpha\) adalah percepatan sudut.
- \(t\) adalah waktu tempuh.
Percepatan sudut, percepatan sentripetal, dan percepatan tangensial
Dalam materi sebelumnya kita sudah membahas hal ini, sekarang kita akan membahas lebih mendalam.
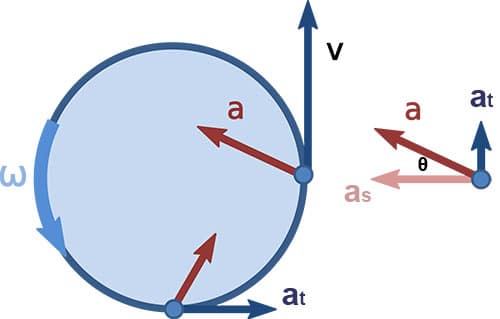
Dalam gambar, terlihat bahwa percepatan total \(a\) memiliki dua buah komponen, yaitu percepatan sentripetal \(a_s\) yang arahnya selalu menuju pusat lingkaran, dan percepatan tangensial \(a_t\) yang arahnya tegak lurus dengan \(a_s\). Di sini benda yang diputar tidak hanya bergerak dalam satu arah, tetapi dalam dua arah (vertikal dan horizontal).
Berikut ini adalah hubungan ketiganya:
- \(a_t = \alpha . r\)
- \(a_s = {\omega}^2.r = \frac{v^2}{r}\)
- \(a = \sqrt{{a_t}^2 + {a_s}^2}\)
- \(\tan \theta = \frac{a_t}{a_s}\)
Catatan bahwa \(a_t\) di sini sering hanya ditulis dengan \(a\) pada gerak lurus, karena \(a_t\) pada gerak melingkar sama saja dengan \(a\) pada gerak lurus. \(a\) dalam gerak melingkar sebenarnya adalah resultan dari \(a_s\) dan \(a_t\).
Agar tidak rancu dengan \(a\) pada gerak lurus, seringkali digantikan dengan simbol \(a_{tot}\).

Mari kita selesaikan contoh soal gerak melingkar berubah beraturan berikut ini:
1. Sebuah kipas yang mulanya diam, dipercepat beraturan selama 10 detik. Kecepatan sudut kipas tersebut 20 rad/s. Besar sudut yang ditempuh kipas selama 10 detik adalah?
Diketahui:
- \({\omega_0} = 0\)
- \({\omega_t} = 20 \ rad/s\)
- \(t = 10 \ s\)
Ditanyakan: \(\theta\) = ?
Jawab:
- \({\omega}_t = {\omega}_0 + \alpha . t\)
- \(20 = 0 + \alpha . 10\)
- \(\alpha = 2 \ rad/s^2\)
- \(\theta = {\omega}_0 . t + \frac{1}{2} \alpha . t^2\)
- \(\theta = 0 . 10 + \frac{1}{2} 2 . 100\)
- \(\theta = 100 rad\)
2. Benda yang semula diam diputar dengan percepatan sudut \(15 \ rad/s^2\). Benda tersebut berada \(10 \ cm\) dari sumbu putar. Tepat pada \(t = 0,4 \ s\) benda mengalami percepatan total sebesar?
Diketahui:
- \(\alpha = 15 \ rad/s^2\)
- \(r = 10 \ cm\)
- \(t = 0,4 \ s\)
Ditanyakan: \(a_{tot}\)
Jawab:
- Untuk dapat menghitung \(a_{tot}\) diperlukan \(a_s\) dan \(a_t\)
- \(a_t = \alpha . r\)
- \(a_t = 15 . 0,1 \ = \ 1,5 \ m/s^2\)
Kita perlu menghitung kecepatan sudut pada waktu ke t untuk dapat menghitung \(a_s\)
- \({\omega}_t = {\omega}_0 + \alpha . t\)
- \({\omega}_t = 0 + 15 . 0,4\)
- \({\omega}_t = 6 \ rad/s\)
- \(a_s = {\omega}^2 . r\)
- \(a_s = 6^2 . 0,1 \ = \ 3,6 \ m/s^2\)
- \(a_{tot} = \sqrt{{a_t}^2 + {a_s}^2}\)
- \(a_{tot} = \sqrt{1,5^2 + 3,6^2}\)
- \(a_{tot} = \sqrt{15,21}\)
- \(a_{tot} = 3,9 \ m/s^2\)
Kutip materi pelajaran ini:
Kontributor Tentorku, 2015, https://www.tentorku.com/gerak-melingkar-berubah-beraturan-gmbb/ (diakses pada 27 Jul 2024).
Materi pelajaran ini bukan yang Anda butuhkan?
Anda bisa mengirimkan saran pada Tentorku di akun fb/twitter/google kami di @tentorku.
Topik dengan voting komentar terbanyak akan mendapatkan prioritas dibuatkan pembahasan.