Kinematika (2D): Gerak Parabola | Gerak Peluru

Pada bagian sebelumnya kita telah membahas mengenai dasar-dasar kinematika gerak translasional (dua dimensi) dengan analisis vektor, sekarang kita akan melanjutkan pembahasan tersebut dengan kasus pada gerak parabola atau sering disebut juga dengan gerak peluru. Gerak ini termasuk ke dalam gerak dua dimensi, karena memiliki komponen gerak vertikal dan gerak horizontal.

Definisi gerak parabola adalah bentuk gerak di mana suatu objek atau patikel (disebut peluru) dilemparkan dekat permukaan bumi, dan bergerak sepanjang lintasan melengkung yang hanya dipengaruhi aksi gaya gravitasi. Satu-satunya gaya yang signifikan yang mengenai objek adalah gaya gravitasi, yang memiliki arah ke bawah (menuju pusat bumi), yang menyebabkan arah percepatan ke bawah. Tidak ada gaya horizontal yang mempengaruhi gerak horizontal objek pada gerak peluru ini. ^[1]

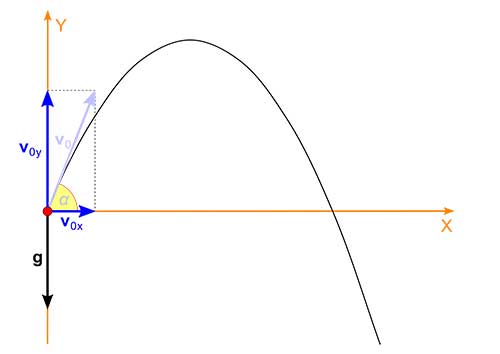
Perhatikan gambar di atas. Apabila peluru diluncurkan dengan kecepatan awal \(\mathbf{v}_0\), maka vektor kecepatan dapat dituliskan dengan

\(\mathbf{v}_0 = v_{0x}\mathbf{i} + v_{0y}\mathbf{j}\)

Sehingga komponen \(v_{0x}\) dan \(v_{0y}\) dapat dicari apabila sudut \(\theta\) diketahui

• \(v_{0x} = v_0 \cos\theta\)
• \(v_{0y} = v_0 \sin\theta\)

Keterangan:

• \(v_0\) adalah kecepatan awal dua dimensional
• \(v_{0x}\) adalah kecepatan awal pada sumbu-x (horizontal)
• \(v_{0y}\) adalah kecepatan awal pada sumbu-y (vertikal)

*Apabila bingung dengan penjelasan ini, saya sarankan untuk membaca bagian vektor.

Besaran Kinematika dari Gerak Parabola / Gerak Peluru

1. Percepatan
Seperti yang telah kita ketahui, tidak ada gaya dari luar yang mengenai gerak pada sumbu-x (horizontal), sehingga \(a_x = 0\). Namun, gerak pada sumbu-y dikenai oleh gaya gravitasi yang arahnya ke bawah sehingga \(a_y = -g\).

Oleh karena itu gerak pada sumbu-x adalah gerak lurus beraturan (GLB), sedangkan gerak pada sumbu-y adalah gerak lurus berubah beraturan (GLBB).

*Apabila masih bingung dengan penjelasan di atas, saya sarankan membaca bagian GLB dan GLBB.

2. Kecepatan
Untuk menghitung komponen kecepatan horizontal dan vertikal pada saat \(t\), dapat menggunakan rumus ini:

• \(v_x = v_0 \cos\theta \quad\) atau \(\quad v_x = v_{0x}\)
• \(v_y = v_0 \sin\theta - gt\quad\) atau \(\quad v_y = v_{0y} - gt\)

Keterangan:

• \(v_x\) adalah kecepatan horizontal pada saat \(t\)
• \(v_y\) adalah kecepatan vertikal pada saat \(t\)
• \(g\) adalah percepatan gravitasi \(9,8 \ m/s^2\)
• \(t\) adalah waktu (sekon)

Seperti biasa, untuk mendapatkan besar (resultan) kecepatan dapat menggunakan teorema pythagoras:

\[v = \sqrt{{v_x}^2+{v_y}^2}\]

3. Perpindahan
Untuk menghitung perpindahan horizontal dan vertikal pada saat \(t\), dapat menggunakan rumus ini:

\(x = v_0.t \cos\theta \quad\) atau \(\quad x = v_{0x}.t\)
\[y = v_0.t \sin\theta - \frac{1}{2}g.t^2\]

atau

\[y = v_{0y}.t - \frac{1}{2}g.t^2\]

Seperti biasa, untuk mendapatkan besar (resultan) perpindahan dapat menggunakan teorema pythagoras:

\[\Delta r = \sqrt{x^2+y^2}\]

Sekarang setelah kita mengetahui konsepnya, waktunya untuk berlatih soal!

1. Sebuah benda diluncurkan dari tanah dengan sudut tertentu, 3 detik kemudian kecepatan \(\mathbf{v}\) adalah \(20 \ m/s, -4 \ m/s\). Carilah (a) berapa jauh maksimum yang dapat ditempuh (horizontal), dan (b) berapa tinggi maksimum yang dicapai (vertikal), gunakan \(g = 10 \ m/s^2\). ^[2]

Diketahui:
Pada \(t = 3 \ s\)
\(v_x = 20 \ m/s\)
\(v_y = -4 \ m/s\)

Ditanyakan:
a) \(x\)
b) \(h_{max}\)

Jawab:
Kita terlebih dahulu harus mencari waktu dari benda diluncurkan sampai mencapai titik tertinggi dan sampai mencapai tanah, untuk itu kita harus menghitung komponen vertikal terlebih dahulu.

\(v_y = v_{0y} - g.t\)
\(-4 = v_{0y} - 10.3\)
\(v_{0y} = 26 \ m/s\)

Setelah didapatkan kecepatan awal pada sumbu-y kita dapat menghitung waktu sampai kecepatan menjadi nol.

\(v_y = v_{0y} - g.t\)
\(0 = 26 - 10t\)
\(10t = 26 \ \Rightarrow t = 2,6 \ s\)

Ingat bahwa \(t = 2,6 \ s\) adalah waktu mencapai ketinggian maksimum, gunakan ini untuk mencari \(h_{max}\). Jarak horizontal terjauh \(x\) didapatkan dari menggunakan waktu dari benda dilempar sampai menuju tanah, yaitu dua kali waktu untuk mencapai ketinggian maksimum \(t = 5,2 \ s\).

a) Untuk mencari \(x\) kita membutuhkan \(v_{0x}\), karena kecepatan pada GLB adalah konstan, maka \(v_x = v_{0x} = 20 \ m/s\)

\(x = v_{0x}.t\)
\(x = 20 . 5,2 = \ 104 \ m\)

b) Untuk mencari \(h_{max}\) gunakan rumus GLBB pada \(t_{hmax} = 2,6 \ s\)

\[y = v_{0y}.t - \frac{1}{2}g.t^2\] \[y = 26.2,6 - \frac{1}{2}10.2,6^2\] \[y = 67,6 - \frac{1}{2}.67,6 = \ 33,8 \ m\]

Dengan bahasa sederhana, kita dapat mengatakan gerak parabola ini sebenarnya hanyalah gerak campuran antara gerak horizontal (GLB) dan gerak vertikal (GLBB). Komponen vertikal dan horizontal itulah yang menyebabkan lintasan menjadi berbentuk melengkung, perlu diingat pokok bahasan gerak parabola ini aplikatif apabila hanya mempertimbangkan gaya gravitasi.

Dalam dunia nyata akan kita jumpai bahwa lintasan dapat berubah-ubah karena dipengaruhi oleh gaya gesek udara termasuk magnus effect. Mari kita lihat teori yang menjelaskan tendangan pisang legendaris Roberto Carlos 🙂